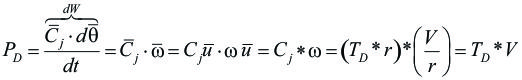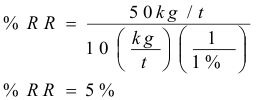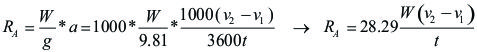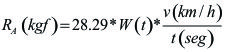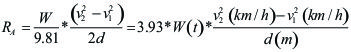5.- DINÁMICA DE LAS MÁQUINAS DE MOVIMIENTO DE TIERRAS.
Este aspecto es fundamental, pues los Ingenieros deben dominar la dinámica del movimiento y de trabajo de las principales maquinarias, para saber cuáles son los factores y fuerzas que permiten obtener un mayor rendimiento, es decir, el aprovechamiento máximo de la capacidad de trabajo de los equipos de construcción, lo cual posee una evidente repercusión técnico-económica en la eficiencia constructiva de las obras horizontales y gran influencia en las obras verticales.
La importancia técnica-económica del conocimiento y dominio de la Dinámica de estas máquinas de construcción, descansa en que los Ingenieros estén conscientes de las condiciones que deben existir para que cualquier maquinaria de construcción que se desplace a trabajar, del cumplimiento de las dos condiciones básicas para realizar un trabajo útil de empuje o tracción, lo cual puede decidir en la selección de uno u otro equipo para acometer un trabajo, lo que a su vez puede influir en una mayor o menor economía en la ejecución del mismo, en la compra o adquisición de determinadas máquinas; así como para la determinación de los rendimientos de las maquinarias. Todo lo anterior demuestra la importancia del estudio y dominio de esta temática para este profesional de la construcción
El objetivo de este acápite es la determinación de la velocidad de traslación a la que pueden funcionar las máquinas de movimiento de tierras durante su trabajo. Para dicho cálculo será necesario conocer las características de la máquina (peso, potencia), y las del terreno sobre el que se desplaza y su pendiente.
Se estudiará los tipos de tracción de las máquinas y los tipos de resistencia al movimiento.

Fig. No 2.3.1: ¿Se desplazarán las máquinas?
5.1.- ESFUERZO TRACTOR
Conceptos Básicos:
El torque y la potencia son dos indicadores del funcionamiento del motor, nos dicen qué tanta fuerza puede producir y con qué rapidez puede trabajar.
Torque y Potencia (Motor) - PREZI (Recuperado de https://prezi.com/p/gkid3ir-sbas/torque-y-potencia-motor/)
a).- Torque: Es la fuerza con la cual se gira un objeto, recordemos que el motor produce fuerza en un eje (Cigueñal) que se encuentra girando.
Torque y Potencia Maquinaría - PREZI (Recuperado de https://prezi.com/kuxplqedvhp-/unidad-1/)
Se llama Torque máximo a la mayor cantidad de fuerza de giro que puede hacer el motor.
b).- Potencia: La potencia indica la rapidez con que puede trabajar el motor, se define: "Como la capacidad de ejecutar trabajo a una velocidad determinada" y se expresa en Joule/seg, es decir en Watt, según el Sistema Internacional de Unidades (S.I.).
Un motor tiene torque máximo y potencia máxima y en los motores de combustión interna estos no se presentan a las mismas revoluciones.
Potencia - PREZI (Recuperado de https://prezi.com/wtqeohthjx_h/potencias/)
Las Unidades de Medida fundamentales son:
- U.M. de Potencia:
1 Watt = 1 Joule/seg. (El watt es la U.M. oficial según el S.I. para la Potencia).
1 Caballo de Fuerza (HP) = 735,499 Watt.
Luego: 1 HP = 0,736 Kilo Watt = 0.736 KW
Como 1 Caballo Vapor es igual a 0,98 HP, se adoptará en los problemas que:
1 CV = 1HP, lo que garantiza suficiente exactitud en los cálculos.
- U.M. de Fuerza:
Se expresarán generalmente en kilogramos-fuerza (kgf), en el S.I. en Newton (N).
Se adoptará que: 1kgf = 10N.
c).- Potencia Nominal (Pn): Es la que se obtiene en “el extremo del cigüeñal cuando el motor se encuentra en servicio continuo y a la máxima velocidad compatible con su resistencia mecánica”. El valor de dicha potencia se mide de varias maneras en un Banco de Pruebas: por el Sistema Dinamométrico, por el Freno de Prony, el Molinete, etc. (campo de acción de los Ingenieros Mecánicos). Los fabricantes dan, generalmente, varias curvas correspondientes a los diferentes servicios previstos, es decir diferentes velocidades de rotación, etc.
¿Pero esta Potencia (Pn) es la que llega al sistema de rodaje del equipo?, es obvio que la respuesta es negativa; parte de esta se pierde en el sistema de transmisión, por los desgastes y por efecto de la temperatura y la altitud a la que se encuentre la máquina, etc.
Se utiliza también la potencia correspondiente al par máximo. En general, este valor difiere notablemente del precedente. Hay también un valor de la potencia que corresponde al mínimo del consumo específico del motor, ver fig.

Curvas de potencia, par y consumo de un motor en función del régimen de revoluciones.
Curvas de Potencia y Torque - PREZI (Recuperado de https://prezi.com/lmwhzvnbvwxx/curvas-de-potencia-y-torque/)
Las Unidades de Medida fundamentales son:
La potencia útil de un motor se transmite a las ruedas por medio de diferentes órganos de transmisión, entre los cuales está el cambio de velocidades, este tiene por finalidad adaptar el número de revoluciones a que el motor desarrolla toda su potencia a la velocidad de traslación del motor. A potencia constante, los esfuerzos producidos en las ruedas motrices y en la barra de tracción serán tanto mayores cuanto más elevada sea la relación entre el número de vueltas de las ruedas o de las orugas.
Así pues, el esfuerzo de tracción disponible es la cantidad en kilogramos fuerza que un motor puede entregar al punto de contacto de las ruedas motrices con el suelo. Este tipo de tracción es independiente del patinaje que puedan sufrir las ruedas motrices en determinados terrenos.
Precisamente la potencia que posee el equipo en su sistema de rodaje se denomina Potencia Motriz (Pm), llamada también Potencia Disponible (PD) y siempre poseerá una magnitud menor que la Nominal (Pn) lo cual puede determinarse según la expresión siguiente:
![]()
Determinación de los factores (al producto en conjunto se le llama eficiencia de transmisión):
- Factor de Reducción por Desgaste (Nu).
Nu: Factor de reducción de la potencia nominal debido al desgaste que sufren los elementos y piezas componentes de las máquinas, lo que puede originar afectaciones de hasta un 10% - 15% .
En los cálculos se adoptará:
Nu = 0,90 ~ 1,00 Equipos Nuevos (hasta varios cientos de horas de uso).
Nu = 0,85 ~ 0,90 Equipos de Uso (varios millares de horas de uso).
- Factor de Transmisión (Nt).
Factor de reducción de la potencia nominal, que tiene en cuenta las pérdidas de potencia que se produce al transmitirse la potencia del motor hasta el sistema de rodaje, tal como se explicó anteriormente al describir el mecanismo de la transmisión, llegando a perderse entre un 15% - 20%.
Para las velocidades directas (velocidad máxima para el caso de las máquinas de movimiento de tierra) es menor la pérdida que para otras velocidades.
Se adoptará entonces:
Nt = 0,85 para velocidad directa (está desembragado el equipo => menores pérdidas de hasta el 15%)=> Se adoptará que Vdirecta = Vmáxima (MMT).
Nt = 0,80 para velocidades restantes (mayores pérdidas de hasta el 20%).
- Factor de Pérdidas por efectos de la Temperatura y la Altitud (TA).
Cuando una máquina accionada por motor diesel funciona a grandes altitudes, se produce un descenso de potencia debido a que disminuye la densidad del aire , afectando a la relación gas-oil/aire en la cámara de combustión del motor. Esta pérdida de potencia produce la correspondiente disminución de tracción en la barra de tiro o en las ruedas propulsoras.
Generalmente los fabricantes brindan como dato la Potencia Nominal (Pn) a una “temperatura de 15° celsius y una altitud coincidente con el nivel medio del mar (n.m.m.)”, para este caso no hay afectación. (TA =1).
Para otras situaciones diferentes se determinará de acuerdo al manual del fabricante, ya que para disminuir los efectos de estos se ha acoplado mecanismos como el turbo compresor.
Ejemplo, del Manual de Rendimiento CAT Ed. 40:
En caso contrario, para estimar los rendimientos de los motores deben seguirse los siguientes criterios:
- Motores diésel de 4 tiempos con aspiración natural
Sin pérdidas hasta 300 m de altitud. Reducción de fuerzas de tracción del orden del 3% por cada 300 m adicionales.
- Motores diesel de 2 tiempos con aspiración natural
Entre el nivel del mar y 1800 m de altitud, reducciones de los esfuerzos de tracción del orden de 1,5% por cada 300 m. Sobre 1800 m, del 3% por cada 300 m.
- Motores turboalimentados de 2 y 4 tiempos
Sin pérdidas apreciables desde los 1500 m hasta los 3000 m sobre el nivel del mar. Para otras alturas se recomienda consultar las especificaciones dadas por los fabricantes.
Ejemplo de Factores de corrección de la Potencia Nominal de los Motores según la Altitud sobre el nivel medio del mar y la Temperatura Ambiental:
Fuente: "Máquinas de Movimiento de Tierras: Criterios de Selección Francisco Ballester y Jorge Capote"
Nota.- La reducción de potencia por altura, en el cálculo de la producción interviene directamente en el tiempo de ciclo de producción, aumentamdole en el mismo porcentaje de su disminución.
d).- Fuerza Motriz: Para comprender qué se entiende por Fuerza Motriz, se empleará el ejemplo de un disco que gira libremente sobre su eje, en el siguiente esquema o diagrama del cuerpo libre, se observan “La Fuerza Motriz (Fm o TD) que, es una de las fuerzas del par de fuerzas (par motriz) que hace posible que la rueda gire, sobre su eje.”:
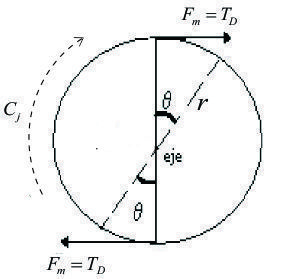
Donde:
Cj: Momento o par Motriz.
TD: Fuerza Motriz ó Tracción Disponible ó Fuerza Motriz Disponible.
r: Radio de la rueda (m).
Si la potencia producida por un par es:
Del análisis se desprende que: “a menor velocidad mayor fuerza y viceversa”.
Debe destacarse que habrá una magnitud de Fuerza Motriz, para cada Velocidad de trabajo, además a menor velocidad habrá mayor fuerza de tracción para la misma potencia disponible.
Las expresiones que se determinen a partir de lo deducido, dependerá de las unidades a utilizar.
De acuerdo con la fórmula anterior, la fuerza de tracción disponible sería variable para cada velocidad, y alcanzaría un máximo para una velocidad muy pequeña, que podría considerarse como tendiendo a cero. Pero esta fuerza resulta inalcanzable por una serie de razones, primero, por la, existencia en el sistema de transmisión de potencia de un número finito de relaciones de engranajes, con las pérdidas citadas por rozamientos internos, y segundo, porque el esfuerzo de tracción real que puede realizar una máquina depende del peso que gravita sobre el eje propulsor y del coeficiente de adherencia de los neumáticos sobre el suelo.
Comparación de la curva característica de potencia constante con la curva real de transmisión de potencia.
Luego debemos tener muy en claro que, el motor primario debe entregar suficiente fuerza tractiva que logre vencer la resistencia total al movimiento. La fuerza máxima que debe ser aplicada por un motor primario está limitada ya sea por la máxima potencia del generador de energía o la máxima tracción que existe entre los neumáticos o las orugas y la superficie de soporte. La mínima energía de salida o generada en la tracción es la máxima fuerza utilizable.


Fig. No 2.3.2: Potencia del motor a la barra de tiro
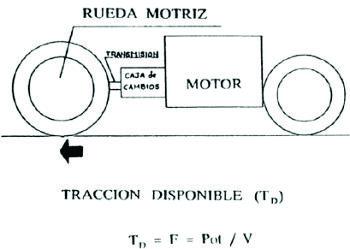
5.1.1.- Tracción Disponible (TD).
Maquinaria pesada - Ecuación del Movimiento (Recuperado de https://prezi.com/9ghnhcbbl_y1/maquinaria-pesada-y-movimientos-de-tierra-unidad-2/)
Toda máquina cuenta con una fuerza motriz disponible (Fuerza de empuje) la cual se conoce como tracción disponible, que es la potenca bruta máxima que puede entregar. Para la realización de un trabajo, la máquina cuenta con una fracción de la fuerza motriz disponible, que depente de la tracción del camino (Fuerza de agarre), la cual se conoce como tracción utilizable.
Para llevar a cabo una actividad tenemos la tracción motriz requerida, que es la necesaria para mover la máquina, es básicamente la suma de la resistencia a la rodadura y la resistencia a la pendiente (despreciando la resistencia a la inercia y al aire), que contituyen la resistencia total o "pendiente compensada (%).
Luego una máquina dispondrá de una potencia para desplazarse producida por el motor (unidad motriz) y que se aplicará en las ruedas motrices mediante la transmisión. Al esfuerzo, producido por el motor y la transmisión, se denominará tracción disponible o esfuerzo de tracción a la rueda, siendo ésta aplicada al diámetro total del neumático, o en el caso de cadenas al diámetro de la rueda cabilla(rueda motriz por ende a la barra de tiro). La definición de esta tracción es, por tanto, la fuerza que un motor puede transmitir al suelo.
La tracción disponible puede calcularse de forma aproximada para cada velocidad de marcha mediante las expresiones (dependiendo de las unidades de potencia):
La eficiencia de transmisión, también llamado eficiencia mecánica, es la relación entre potencia que llega al eje motriz y potencia del motor. Los valores aproximadas más comunes se encuentran entre el 70% y el 85% (los cuales deben ser cálculados de acuerdo a lo mencionado líneas arriba, siendo lo más aproximadas a la realidad).
Fig. No 2.3.3: Tracción disponible
Equilibrio de fuerzas.- Si un equipo se mueve a velocidad constante (se utliza tablas para encontrar la velocidad promedio y considerarlo como constante, asi encontrar el tiempo de ciclo), la sumatoria de fuerzas externas en la maquinaria será nula, por lo tanto la suma de las fuerzas resistente (RT) es igual a la fuerza de empuje (Tracción Disponible).
Si: TU > RT, entonces RT = TD
Fig. No 2.3.3A: Equilibrio de fuerzas.
5.1.2.- Fuerzas Resistentes al Movimiento, o la Tracción Total (RT).
Se le considera como un factor limitante del rendimiento; como se ha observado, un equipo puede mover sus ruedas o zapatas a partir de la potencia generada en su motor, teniendo presente las pérdidas que interiormente suceden en él mismo y dada la altitud y temperatura ambiental; pero no se ha considerado que ese equipo estará en contacto con distintas superficies, que tendrá que subir elevaciones con una pendiente determinada, que tendrá que vencer la resistencia que ofrece el aire y la inercia al modificarse la velocidad de traslación durante la marcha.
Si despreciamos las resistencias a la aceleración y al aire, la Resistencia al movimiento del equipo, es la suma de la Resistencia a la Rodadura (RR) más Resistencia a la Pendiente (RP):
Fig. No 2.3.9: ¿Habrá suficiente potencia utilizable o necesaria, para vencer la resistencia total o la tracción?
Si Ud. está en obra, o está tratando de seleccionar el equipo para una obra futura, ¿cómo determina si una máquina puede satisfacer los requisitos de obra?. por ejemplo, ¿puede un cargador de cadenas sacar una carga de la excavación de un sótano, si el terreno está mojado?. Primero, hay que tomar en cuenta la potencia necesaria para que suba el cargador por la rampa. Segundo, ¿tiene la máquina potencia necesaria?, si no tiene, debe disminuir la carga, disminuir la pendiente de la rampa o utilizar una máquina más potente. Supongamos que la máquina tenga potencia necesaria, ¿es toda la potencia utilizable?, o ¿cómo va afectar la rampa en la tracción de la máquina?
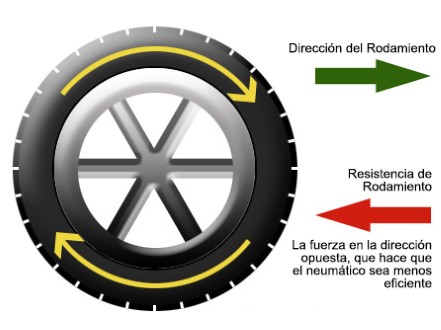
5.1.2.1.- Resistencia a la Rodadura (RR).
La resistencia a la rodadura se define como la oposición al movimiento de una máquina como consecuencia de la deformación del suelo, las flexiones de los neumáticos y los rozamientos internos de los propios mecanismos del equipo.
Esta resistencia varía considerablemente de acuerdo al tipo y condición de la superficie de la vía por la que el vehículo se mueve. Las superficies muy suaves presentan una mayor resistencia en comparación con las superficies duras como el pavimento de concreto. Para vehículos que utilizan neumáticos, la resistencia a la rodadura varía con el tamaño, presión, y el diseño de las ruedas. Para los equipos que se mueven sobre orugas como los tractores, la resistencia varía principalmente con el tipo y condición de la superficie de la vía.
Por lo tanto, la principal resistencia al movimiento del equipo en una superficie nivelada se denomina resistencia de rodadura (Rolling Resistance o RR). Varias fuerzas afectan la Resistencia a la Rodadura, las más importantes son: Fricción interna (Fri), Flexión del Neumático(F/N) y penetración del Neumático (PN). Por lo que podemos decir la rodadura depende del tipo de terreno y tipo de elementos motrices, neumáticos o cadenas, por la que muchas veces se utilizan tablas para poder encontrar los factores de resistencia a la rodadura (coeficientes de resistencia a la rodadura), así como del peso bruto del vehículo.
RR = Fri + F/N + PN
Fig. No 2.3.10: Resistencia a la rodadura
a.- Fricción Interna (Fri) .- Es la resistencia de las condiciones del eje motriz, desde el volante del motor hasta los mandos finales.
b.- Flexión del Neumático (F/N) .- Es la resistencia por la deformación de las paredes y rodadura de los neumáticos a medida que éste gira.
La experiencia ha demostrado, que una máquina a la que se presta servicio regularmente la Fricción Interna y la Flexión del neumático se consideran como un factor constante (20 kg/t. métrica o 40 lb/ton). Así que sin tomar en cuenta ningún otro factor, son necesarios 20 kg (40 lb) de tiro o de empuje por cada tonelada de Peso Bruto del Vehículo (PBV).
c.- Penetración de los Neumáticos (PN).- El estado del camino de acarreo afecta también la Resistencia a la Rodadura. Cuando los caminos de acarreo se mantienen en buen estado, las unidades de acarreo se pueden mover con mayor velocidad. Esto reduce los ciclos de trabajo y aumentan la Producción. En caminos en mal estado, los neumáticos se hunden y la máquina pierde velocidad. La penetración del neumático (PN) aumenta la Resistencia a la Rodadura. La Experiencia nos señala, que, por cada 25 mm (1 pulg) de penetración de neumático, la máquina debe vencer una resistencia adicional de 15 kg/t (30 lb/ton) del PBV, ó 1.5% de pendiente favorable.
Fig. No 2.3.11: Penetración de los neumáticos
Fig. No 2.3.12: Resistencia a la Rodadura
El factor de resistencia a la rodadura (fR) se puede expresar en kg/t (lb/ton) o como el Porcentaje Favorable de la pendiente. Existe una relación directa entre la factor de resistencia expresada en kg/t (lb/ton) y en el Porcentaje:
10 kg/t de fR = 1% de Pendiente Favorable.
20 lb/ton de fR = 1% de Pendiente Favorable.
Por ejemplo, un cargador de ruedas que carga una capa superior húmeda desde la pila, encuentra una factor de Resistencia de Rodadura de 50 kg/t (100 lb/ton). ¿Cuál es el factor de la Resistencia a la Rodadura expresada en Porcentaje?. Según la fórmula:
Regla Empírica:
Fig. No 2.3.13: Regla empírica de resistencia a la rodadura
Como método empírico o aplicación práctica utilizando tablas
Se admite que la resistencia a la rodadura, es proporcional al peso total del vehículo, y se expresa por:
RR = fRx W
RR: Resistencia a la rodadura
fR: Factor de resistencia a la rodadura (kg/t).
W: Peso del vehículo.
Ejemplo 1: Un tractor de ruedas trabaja junto a una draga donde la penetración es de 250 mm (10 pulg). ¿Cuál es al factor de la Resistencia (fR)a la Rodadura (fR) en kg/t (lb/ton)? ¿ O cómo porcentaje de la pendiente? (Recuerde que FRR = Fricción Interna + Flexión del Neumático + Penetración del Neumático)
En lb/ton:
fR = 40 lb/ton + penetración (pulg)*(30 lb/ton)/(1 pulg) = 40 lb/ton + 10*30 lb/ton = 340 lb/ton
En kg/t:
fR = 20 kg/t + penetración (mm)*(15 kg/t)/(25 mm) = 20 kg/t + 250*0.6 kg/t = 170 kg/t
Usando % de la Pendiente:
10 kg/t = Pendiente 1%
20 lb/ton = Pendiente 1%
Podemos cambiar los kg/t (lb/ton) a % de la pendiente:
% de la Pendiente = (170 kg/t)/10 kg/t = 17
Pendiente = 17 %
% de la Pendiente = (340 lb/ton)/20 lb/ton = 17
Pendiente = 17 %
El efecto de la resistencia a la rodadura en vehículos de cadena es insignificante. Aunque existe penetración de las cadenas es ligera y en condiciones normales totalmente insignificante.
La resistencia al rodamiento se expresa usualmente en kgf (libras) del esfuerzo tractivo requerido para mover cada tonelada del peso del vehículo sobre un tipo determinado de superficie. Es muy difícil determinar de manera precisa los valores para los diferentes tipos de superficies y de vehículos, sin embargo los valores de las siguiente tablas son lo suficientemente aproximadas a la realidad.
La resistencia a la rodadura depende del tipo de elementos motrices, neumáticos o cadenas. Los valores más utilizados se recogen en las siguientes tabla:
Tabla N0 2.3.3: Factores de resistencia a la rodadura en porcentaje del peso combinado de la máquina (fR %)
Tipo y condiciones del terreno
Factor (fR %)
Llantas
Orugas
Corriente
Radial
Arena suelta
10.0
10.0
2.0
Camino en asfalto, duro, liso, conservado, que no cede
2.0
1.5
0
Concreto
2.0
1.5
0
Gravilla compactada seca, sin material suelto, no cede
2.5
1.7
0
Gravilla sin compactación pero seca
3.0
2.5
0
Gravilla suelta
10.0
10.0
2.0
Camino en tierra, que se hunde bajo carga, con poca conservación con flexión y penetración de las llantas hasta de 1"
4.0
4.0
0
Camino en tierra, que se hunde bajo carga, con mala conservación, sin riesgo con flexión y penetración de las llantas hasta de 2"
5.0
5.0
0
Camino blando irregular con surcos o canales sin estabilizar con flexión y penetración de las llantas de 4"
8.0
8.0
0
Camino blando irregular con surcos o canales sin estabilizar con flexión y penetración de las llantas de 8"
14.0
14.0
5.0
Camino muy blando irregular con fango sin flexión pero con penetración de las llantas de 12"
20.0
20.0
8.0
Fuente: Caterpillar
Tabla N0 2.3.4: Factores de resistencia a la Rodadura en fuerza por el peso combinado de la máquina [fR (kgf/t)]
Condiciones del terreno
Factor [fR (kgf/t)]
Llantas
Orugas
Alta presión*
Baja presión
Hormigón liso
17
22
27
Asfalto en buen estado
20 - 32
25 - 30
30 - 35
Camino firme, superficie plana, ligera flexión bajo carga (buenas condiciones)
20 - 35
25 - 35
30 - 40
Camino blando de tierra (superficie irregular con una penetración de neumáticos de 2 a 3 cm)
50 - 70
35 - 50
40 - 45
Camino blando de tierra (superficie irregular, con una penetración de neumáticos de 10 a 15 cm)
90 - 110
75 - 100
70 - 90
Arena o grava suelta
130 - 145
110 - 130
80 - 100
Camino blando, fangoso, irregular o arenoso con más de 15 cm de penetración de los neumáticos.
150 - 200
140 - 170
100 - 120
*Se puede considerar alta presión > 5 kg/cm2, llevando ésta dúmpers y traillas.
Fuente: A. Day.
En la Tabla 2.3.3 y 2.3.4 se recogen los valores más comunes de los factores de resistencia a la rodadura.
Ejemplo 02:
Un volquete con un peso de 36 388 kg sobre una pista horizontal con una resistencia a la rodadura de un 2% debe desarrollar un esfuerzo para vencer esa resistencia antes de ponerse en movimiento de 726 kg (36 288 kg x 0.02). Si el volquete desarrolla un esfuerzo de tracción (disponible) total de 13 000 kg dispondrá de 12 274 kg (13 000 kg menos 726 kg) para realizar el trabajo, si en terreno lo permite.
Un procedimiento para estimar el factor de resistencia a la rodadura fR consiste en medir la profundidad de la huella, " H", dejada por los neumáticos en el firme de la pista . El Factor de Resistencia a la Rodadura será igual a:
fR (kg/t) = 20 ( kg/t) + 6 [kg/(t x cm)] x H (cm)
Ejemplo 03
Así, por ejemplo , el volquete anterior de 32,6 t de capacidad con un peso en vacio de 36,3 t, cuyos neumáticos penetran en el firme 3 cm, permite estimar el siguiente FRR:
fR (kg/t) = 20 + (6 x 3) = 38 kg/t.
La Resistencia a la Rodadura , "RR", se calculará , pues, a partir de:
RR (kg ) = fR (kg/t)x PBV (t).
donde:
PBV = Peso bruto del Vehículo (t)
Si el volquete anterior se desplaza cargado , se tiene:
RR = 38 kg/t x 68,9 t = 2 618 kg
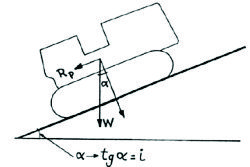
5.1.2.2.- Resistencia a la Pendiente (RP) .- La resistencia a la pendiente es la fuerza debida a la acción de la gravedad cuando un vehículo se mueve por una pista de transporte inclinada, (ver figura). Cuando esa misma máquina, en lugar de ascender, desciende por esa pista, la fuerza de la gravedad ayuda al movimiento del vehículo se conoce como pendiente asistida.
Cualquier equipo que se mueva sobre una superficie inclinada debe generar suficiente fuerza tractiva para sortear la resistencia de la pendiente, que debido al peso origina una fuerza contraria al movimiento, y también la fuerza de resistencia al rodamiento. En la figura 2.3.13 se muestra el efecto de un suelo inclinado.
La expresión de dicha resistencia es:
Y para pendientes de hasta el 20% se puede hacer la siguiente simplificación:
(para ángulos menores a 200)
Fig. No 2.3.14: Descomposición del peso
Siendo (+) si el vehículo sube y (-) si baja.
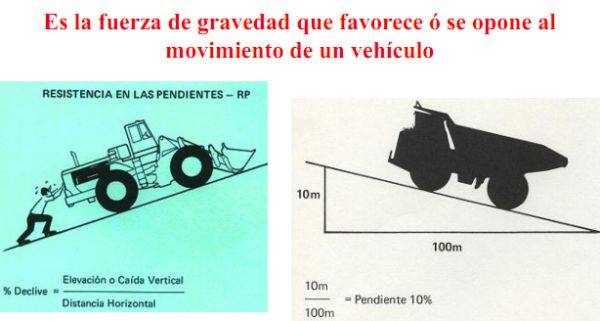
Es la gravedad que debe vencer al subir o bajar una pendiente. Esta trabaja en contra de las máquinas de ruedas y de cadenas (cuesta arriba) o ayuda en pendientes favorables (cuesta abajo). Las pendientes se miden generalmente en tanto por ciento de talud o como la relación entre la elevación de la pista y su longitud en horizontal. Por esto una pista que permite ascender 6 m en 100 m tiene una pendiente del 6%.
Por consiguiente la resistencia en rampa (o la resistencia a la pendiente) es de 10 Kg/t por cada 1% de rampa (o de pendiente). Recíprocamente 1% de pendiente (o de rampa) equivale a 10 Kgf/t de incremento de esfuerzo tractor.
Fig. No 2.3.15: Regla empírica para el cálculo de la resistencia a la pendiente
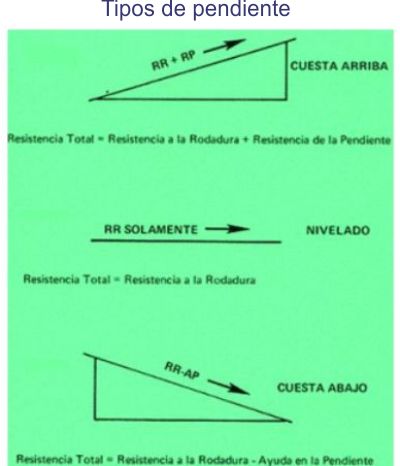
Fig. No 2.3.16: Tipos de pendiente
Peso.- El peso es el factor determinante en la cantidad de fuerza que se precisa para vencer la resistencia a la rodadura y a la pendiente. La fuerza disponible restante servirá para conseguir la aceleración del vehículo.
Se define a la pendiente compensada, como la resistencia total expresada en terminos de pendiente (porcentaje)
Pendiente compensada o efectiva ic (%) = Resistecia a la rodarura (%)
Pendiente Natural (%)
o bien, si también lo expresamos en unidades de fuerza. es:
Resistencia total (kg) = Resistecia a la rodarura (kg)
Pendiente Natural (kg)
En el Ejemplo 03:
Así, el mismo volquete anterior con un peso de 36.288 kg, cuando se desplaza por una pista del 6% de pendiente, debe desarrollar 2.177 kg (36.288 kg x 0,06) de esfuerzo de tracción para vencer esas resistencias. Si se disponía originalmente de 13 000 kg de esfuerzo de tracción, podrá desarrollar el trabajo con 10 823 kg (13 000 kg menos 2 177 kg), en esas condiciones.
ic (%) = 2% + 6% = 8%
RT (kg) = 726 kg + 2 177 kg = 2 903 kg
Se dispondrá entonces de 10 097 kg (13 000 kg menos 2 903 kg) para conseguir la aceleración del volquete.
De todo lo anterior se obtiene que la cantidad de Kg-fuerza de tracción requeridos para mover un vehículo, es la suma de los necesarios para vencer la resistencia a la rodadura y los requeridos para vencer la resistencia a la pendiente, es decir:
ó
Ejemplo:
Dada una máquina cuyo peso es de W = 22 t, la cual se desplaza por una superficie que tiene una pendiente desfavorable de i = 3% y con un coeficiente de resistencia a la rodadura de 50 Kg/t que equivale a una pendiente ficticia del 5%, se pide calcular la resistencia total que tiene que vencer la máquina en sus desplazamientos.
Solución
Dicha resistencia total será:
ó
Nota.- No consideraremos la resistencia a la aceleración como la resistencia al aire, como la hacen la mayoria de los manuales.
5.1.2.3.- Resistencia a la inercia. Esta fuerza se opone al movimiento (o lo favorece) al cambiarse o modificarse la velocidad con que se desplaza el equipo. Es positiva (se opone al movimiento) cuando se acelera y negativa (favorece al movimiento) cuando se va desacelerando o disminuyéndose la velocidad.
Suponiendo una aceleración uniforme para pasar de la velocidad v1 a v2 en un tiempo t:
La resitencia para acelerar la masa de un vehículo de peo W (t) será:
Para v1 = 0 y v2 = v, quedará:
También se puede expresar esta resistencia en función de la distancia recorrida por el vehículo, d(m):
Sustituyendo este valor de la aceleración en la expresión de la resistencia a la aceleración, resulta:
Por ejemplo, si un vehículo, desplazándose cuesta abajo, quiere frenar en una distancia d(m), cuando circule a una velocidad v(km/h), el esfuerzo de frenado será:
Esta resistencia a la aceleración es poco importante en movimiento de tierras, pero en caso de frenado cobra cierta importancia, ya que interesa conocer la distancia o el esfuerzo de frenado del vehículo.
5.1.2.4.- Resistencia al aire.
Esta resistencia no suele tenerse en cuenta, dado que las velocidades de los vehículos y maquinaria de obra son pequeñas y se sabe que la resistencia al aire es proporcional al cuadrado de la velocidad. De modo que:
Siendo v(m/s) la velocidad del vehículo, S la superficie desplazada normal a la dirección del movimiento y K un coeficiente que depende de la forma de la máquina (más o menos aerodinámica) y que esta comprendido entre 0.02 y 0.08.
Sin embargo, contra viento fuerte la resistencia al aire es un factor significativo. La cantidad determinante es el movimiento relativo del aire respecto al vehículo. Si la velocidad de la máquina es de 16 km/h y la velocidad del aire en sentido contrario es de 64 km/h la velocidad relativa resultante será de 80 km/h. La resistencia al aire debera tenerse en cuenta para valores de velocidad relativa superiores a 80 km/h.
Nota.- Muchos autores no toman en cuenta la resistencia a la aceleración así como también la resistencia al aire.
5.1.3.- Tracción Utilizable (TU), o Necesaria, o de Adherencia o simplente Tracción tractiva.
|
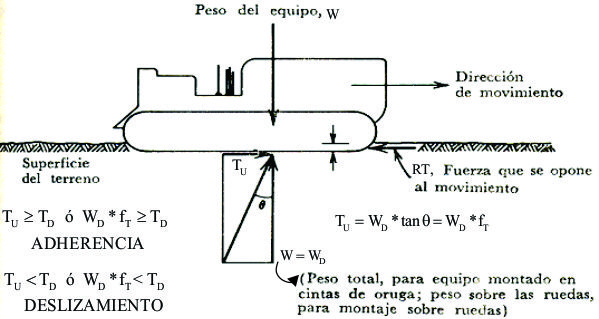
Hasta el presente se ha considerado que existía una adherencia perfecta entre las ruedas o zapatas de los equipos y el suelo, dicho de otra manera, había rodamiento en los puntos de contacto, de los órganos del sistema de rodaje y el suelo, pero es lógico pensar y de hecho en alguna ocasión puede haberse observado, que se produce un patinaje o deslizamiento ¿Cómo determinar que esto sucede? Para ello se parte de analizar el siguiente esquema, que representa una rueda en contacto con el piso o plataforma, así como las fuerzas que intervienen en este caso: Según se puede observar la rueda en su movimiento hacia la izquierda motivado por el Par Motor "Cj" tiene que vencer la resistencia total que es equilibrada por una de las componentes de dicho par; ahora bien, la otra componente aplicada en el punto A de contacto produce una reacción (TU) igual y opuesta, que es precisamente la denominada Fuerza Utilizable o de Adherencia, es decir, “la reacción tangencial del suelo” que es la que permite que el equipo se mueva y sea capaz de desarrollar trabajo sin patinar. Si no existe la adherencia suficiente, la máxima fuerza generada por el motor no puede ser utilizada. Debemos tener en cuenta que las ruedas u orugas se van a deslizar en la superficie, por lo tanto, es muy importante para los operadores el conocimiento del coeficiente de tracción entre los neumáticos u orugas y los diferentes tipos de superficies. La máquina en función de su peso dispondrá de una fuerza determinada que se llama tracción utilizable ó fuerza de adherencia. Esta tracción depende del porcentaje del peso que gravita sobre las ruedas motrices, que es él útil para empujar o tirar del vehículo, y de las superficies en contacto, especialmente área, textura y rugosidad, tanto de las ruedas motrices como del suelo. Para calcular la tracción utilizable se ha de multiplicar el peso total (en caso de pendiente sería su componente normal) que gravita sobre las ruedas motrices por el factor de eficiencia a la tracción o coeficiente de tracción, cuyos valores más comunes se encuentran en tablas, como la que se indica a continuación.
|
Fig. No 2.3.17: Tracción utilizable |
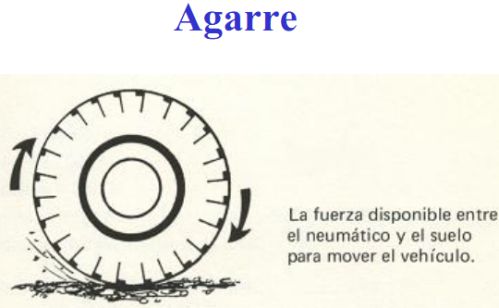


Fig. No 2.3.18: Dependencia de las tracciones
El coeficiente de tracción puede ser definido como el factor que puede multiplicarse por la carga total en las ruedas u orugas para determinar la máxima fuerza tractiva posible entre las ruedas u orugas y la superficie justo antes de ocurrir el deslizamiento del equipo en cuestión. Por ejemplo, las ruedas de un camión se encuentran en un camino de arcilla negra seca, y la presión total entre los neumáticos y la superficie del camino es de 8000 lb. En una prueba tratando de encontrar la fuerza que debe aplicarse para que el camión pueda desplazarse se encontró que este desplazamiento ocurrió cuando la fuerza tractiva entre los neumáticos y la superficie era de 4800 libras. Por lo tanto el coeficiente de tracción es de 4800 / 8000 = 0.60.
El efecto de un tipo específico de superficie indica los Factores de Tracción (fT) o Coeficiente de Tracción (COT), la relación de ésta con el peso, indica la tracción utilizable en las ruedas impulsoras
Tabla N0 2.3.1: Factores de Tracción (fT) o Coeficiente de Tracción (COT)
Material del piso |
Factores de tracción |
|
Neumáticos |
Orugas |
|
Arena húmeda |
0.40 |
0.50 |
Arena seca |
0.20 |
0.30 |
Arena suelta |
0.27 |
0.30 |
Asfalto |
0.90 |
- |
Camino en greda húmeda |
0.45 |
0.70 |
Camino en greda seca |
0.55 |
0.90 |
Cantera |
0.65 |
0.55 |
Carbón |
0.45 |
0.60 |
Concreto/Hormigón |
0.90 |
0.45 |
Gravilla suelta |
0.35 |
0.50 |
Marga arcillosa seca (*) |
0.55 |
0.90 |
Marga arcillosa mojada |
0.55 |
0.70 |
Marga arcillosa con surcos |
0.40 |
0.70 |
Terreno lodoso |
0.25 |
0.25 |
Tierra firme |
0.55 |
0.90 |
Tierra suelta |
0.45 |
0.60 |
Tierra suelta seca |
0.40 |
0.60 |
Fuente: Fiat, Caterpillar y Maquinaria y equipo de construcción del Ing. Jaime Ayllon
(*) Marga: material compuesto de arcilla y carbonato de calcio, tiene color grisáceo y se utiliza para la fabricación de cemento.
En el cálculo de la adherencia hay que tener en cuenta el número de ruedas motrices y la carga soportada por las mismas, que se denomina peso adherente.
En los vehículos que llevan rueda motrices y ruedas portantes se puede admitir en primera aproximación que las ruedas motrices soportan entre 1/2 y 2/3 de la carga total.
En movimiento de tierras hay tendencia a elegir, siempre que sea posible, maquinaria de tracción total, es decir, tracción a todos los ejes; en el caso de camiones de volteo y camiones de volteo articulados, que se verán en el acápite correspondiente, la tracción puede estar aplicada al eje de dirección y a los posteriores.
Hoy todas las cargadoras son de tracción total, es decir, a los dos ejes, y esto se simplifica con el sistema articulado, en donde la dirección se realiza actuando en la articulación con cilindros hidráulicos, en vez de poner los dispositivos con la complejidad mecánica que llevan los tractores agrícolas con tracción también al eje de dirección delantera, en los cuales no se puede obviar este problema al ser rígidos.
En los tractores y cargadoras de orugas todo su peso se da para el cálculo de la tracción utilizable.
Existe una relación entre la fuerza de tracción, la velocidad de desplazamiento y las RPM del motor, si se tiene una transmisión directa (lo que comúnmente se conoce como caja de cambios), se puede hacer una tabla donde se relaciona el cambio en el que se encuentra la transmisión, la velocidad de desplazamiento y la fuerza máxima de tracción (la que se desarrolla en el cambio primera, con el torque más alto del motor y por lo tanto en la velocidad de desplazamiento más baja) y las fuerzas nominales de tracción (son las que se desarrollan con la potencia nominal del motor y las revoluciones (RPM) nominales), un ejemplo de esta tabla, es la siguiente:
Tabla N0 2.3.2: Relación de fuerzas de tracción y velocidades de desplazamiento
Cambio o marcha |
Velocidad de desplazamiento (km/h) |
Fuerza máxima de tracción (kg.) |
Fuerza nominal de tracción (kg.) |
Primera |
2.5 |
34500 |
27600 |
Segunda |
3.5 |
- |
19700 |
Tercera |
4.9 |
- |
14100 |
Cuarta |
6.4 |
- |
10780 |
Quinta |
8.9 |
- |
7670 |
sexta |
12.9 |
- |
5350 |
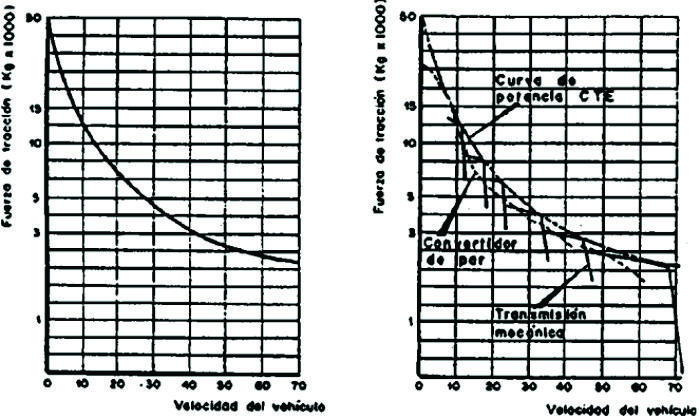
La mayoría de las máquinas se consiguen con el sistema convertidor de torque y servo transmisión y la relación entre la fuerza de tracción y la velocidad de desplazamiento no se puede hacer en una forma directa, por eso los fabricantes lo hacen por medio de gráficas como la siguiente:
Gráfico N0 2.3.1: Velocidad de desplazamiento Vs Tracción en la barra
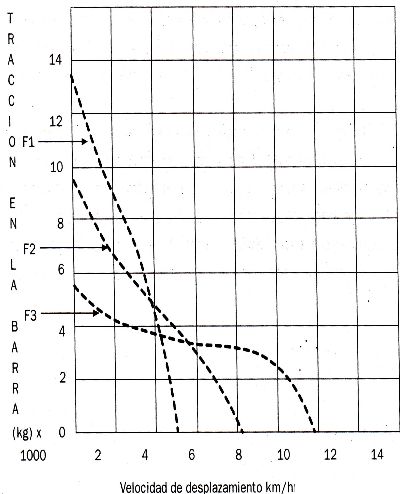
Cada curva punteada (F1, F2, F3) representan una relación diferente de los engranajes o sea el cambio en que se encuentra la transmisión, en el eje X va la velocidad de desplazamiento y en el eje Y va la tracción de la barra de tiro o llantas.
Existen otras gráficas para las moto traíllas y volquetes, la aplicación de estas gráficas se verá cuando se calcule la producción de las máquinas.
|
En caso de pendiente su peso sería su componente normal, La tracción utilizable es independiente de la potencia del motor y se calcula mediante la expresión: TU = WDx fT Siendo WD el peso que soportan las ruedas motrices y fT el coenficiente de tracción. |
Fig. No 2.3.19: Descomposición del peso |
Ejemplo:
¿Cuál es la potencia Utilizable de un tractor de cadenas de 22 700 kg en arena húmeda?
Potencia Utilizable = 0.50*22 700 = 11 350 kg
5.1.4.- Balance entre Tracción Disponible y Tracción Utilizable.
|
Una vez estudiados los tipos de tracción habrá que ver el movimiento del vehículo. Dicho movimiento se basa en la reacción de sus ruedas o cadenas sobre el terreno, al cual le transmite el esfuerzo TD que produce el par motor. Si el esfuerzo de tracción TD es mayor que el esfuerzo máximo de reacción del terreno TU se produce el deslizamiento, por lo que las ruedas patinan y la máquina avanza menos o puede llegar a detenerse. Por el contrario cuando TU es mayor o igual que TD hay adherencia entre ruedas y suelo y el vehículo avanza correctamente. De todo lo anterior se deduce que de nada sirve que una máquina tenga un grupo propulsor muy potente (que desarrolla mucha tracción disponible), si no tiene el peso suficiente para conseguir un esfuerzo tractor (tracción utilizable). Por lo tanto, uno de los criterios de elección de una máquina de movimiento de tierras es el de elegir máquinas con un equilibrio entre el grupo moto propulsor y el peso de la misma. Se entiende por grupo moto propulsor el conjunto de motor y órganos de transmisión con sus reductoras. |
"La fuerza disponible o motriz debe ser menor, o a lo sumo igual, que la utilizable o necesaria para que el equipo se mueva sin patinar" Fig. No 2.3.20: Balance entre TD y TU |
De lo antes explicado puede deducirse que si queremos aumentar la adherencia en máquinas sobre neumáticos, se tendrá que:
Emplear un equipo con la mayor cantidad de ruedas motrices posible (de doble tracción o doble eje motriz).
Aumentar la carga (WD) por rueda motriz.
Aumentar el factor de adherencia (TU); empleando neumáticos con dibujos más pronunciados (ruedas “fangueras”), empleando esteras u orugas; colocando polines o tablones debajo de las ruedas, etc.
Este valor no puede utilizarse como parámetro de comparación, ya que depende de muchos factores y su variación es muy grande.
5.2.- Fuerza en la barra de Tiro, de Gancho o Rimpull.
Para que un equipo pueda ejercer un esfuerzo útil es necesario que la potencia nominal de su motor produzca una velocidad (V en Km/h) y una fuerza motriz TD superior a la Resistencia Total (Rto) que se opone a su movimiento. Este exceso de fuerza que queda disponible para realizar un trabajo se denomina: "Fuerza en el Gancho"( Fuerza en la barra de Tiro, en Inglés: "Rimpull") y se determina según:
![]()
![]()
o
![]()
Esta denominación está dada, porque el equipo básico de la gran mayoría de los equipos de construcción es el tractor (de cadenas o sobre neumáticos) y estos poseen un gancho en su parte trasera, donde se puede suponer concentrado el esfuerzo disponible y de ahí que al esfuerzo disponible se le haya denominado así.
Este valor no puede utilizarse como parámetro de comparación, ya que depende de muchos factores y su variación es muy grande.
5.3.- Condiciones Básicas para el Movimiento.
Definida toda las fuerzas que actúan en el movimiento de las máquinas de movimiento de tierras, ahora hay que estudiar las relaciones entre ellas.
En estos momentos se pueden expresar cuáles son las condiciones para el movimiento de un equipo, para lo cual se partirá del siguiente esquema o cuerpo libre:
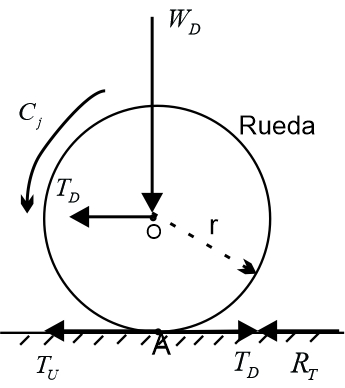
Fig. No 2.3.21: Condiciones básicas para el movimiento
Para que la rueda del equipo se mueva sin deslizar tienen que cumplirse dos condiciones básicas:
Que no exista patinaje o deslizamiento
Que exista fuerza en el gancho disponible para realizar un trabajo útil.
Precisamente, las dos condiciones anteriores son las denominadas “condiciones básicas para el movimiento” y tienen que cumplirse ambas para que un equipo pueda realizar un trabajo útil de empuje o tracción Esto es muy importante, ya que será muy utilizado en la solución de problemas con varias máquinas de movimiento de tierra (en los bulldozeres, las traíllas y las mototraíllas).
|
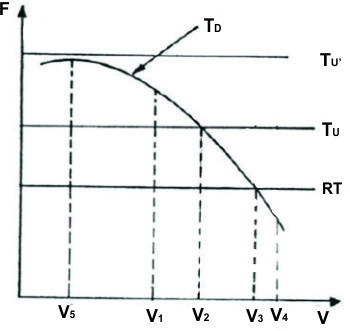
Recíprocamente, conocida la resistencia total y las tracciones utilizable y potencia útil; se puede obtener la máxima velocidad que es capaz de alcanzar la máquina en sus desplazamientos. Todo lo que se ha expresado anteriormente de forma numérica también se puede representar gráficamente en un sistema de ejes coordenados, ver figura, en el cual se colocan en abscisas las velocidades del vehículo y en ordenadas las tracciones, resultando la curva TD para plena potencia del motor y una reducción determinada de la caja de cambios. También se representa la curva TU, que es una recta al ser independiente de las velocidades y puede cortar a la curva TD, o ser exterior TU´. Caso TU:
|
Gráfico No 2.3.2: Velocidades Vs Fuerza de tracciones
|
Caso TU':
V debe ser inferior a V3, pero está limitada inferiormente por el valor V5 de máx. TD, porque a su izquierda hay inestabilidad del vehículo(falta reducción en la caja de cambios).
Los fabricantes de tractores dan gráficas para cada modelo de tractor donde elegida una marcha F1, F2, F3, se obtienen la gama de velocidades y tracción disponible.
Video: CLASE 6 Maquinaria Teorïa Resistencias a Rodadura (Recuperado de https://youtu.be/SsiLKnue4s0)
5.3.1.- Curvas características.
La evaluación de los tiempos de acarreo y retorno en vacío de diferentes equipos de transporte, volquetes y mototraíllas, requiere la utilización de la información suministrada por los fabricantes. La mayoría proporcionan gráficas de tracción-velocidad, también llamadas curvas características, del tipo de las reproducidas en las Gráficos No 2.3.3, 2.3.4 y 2.3.4, cuyo manejo se explica a continuación.
Gráfico No 2.3.3: Velocidades Vs Fuerza de tracciones y Pendientes
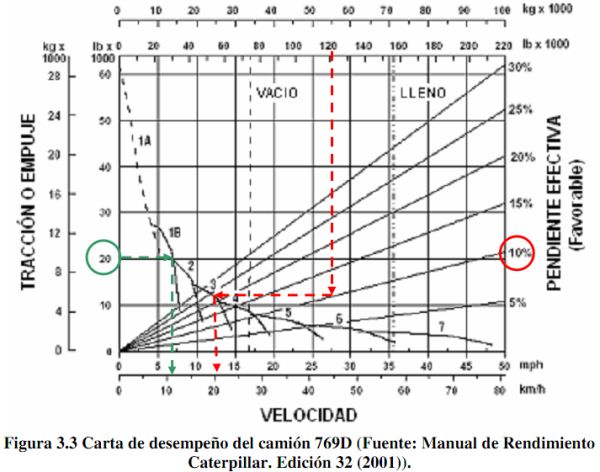
Nota.- Se debe utilizar las cartas de desempeño o cartas de empuje de los manuales, para encontrar las velocidades, como el del Manual de Rendimiento del CAT. Estás gráficas permiten analizar la habilidad de una máquina para realizar una tarea bajo determinadas condiciones de trabajo y carga.
Un volquete con 769D, Gráfico No 2.3.3, se supone que ha de remontar cargado una pendiente adversa del 7% y que la pista presenta una resistencia a la rodadura de 30 kg/t. Se puede afirmar, pues, que la pendiente total compensada es del 10%.
Sobre el gráfico citado, se traza la línea correspondiente al 10% hasta cortar a la vertical de equipo con carga nominal, desde ese punto se traza una línea horizontal hacia la izquierda que corta en un punto a la curva de tercera velocidad, desde donde se baja una vertical que corta al eje de abcisas cercano a los 20 km/h, se puede aproximar a los 21 km/h.
La información obtenida indica que este volquete subiría la pendiente total del 10% en tercera velocidad y con una velocidad máxima de 21 km/h. Si se hubiese prolongado la linea horizontal hacia la izquierda hasta cortar al eje de ordenadas, se habría obtenido la tracción mínima necesaria para remontar la pendiente propuesta, que en este caso sería de unos 6500 kg.
Gráfico No 2.3.4: Curva característica de un volquete de 68 1 de capacidad (KOMATSU).
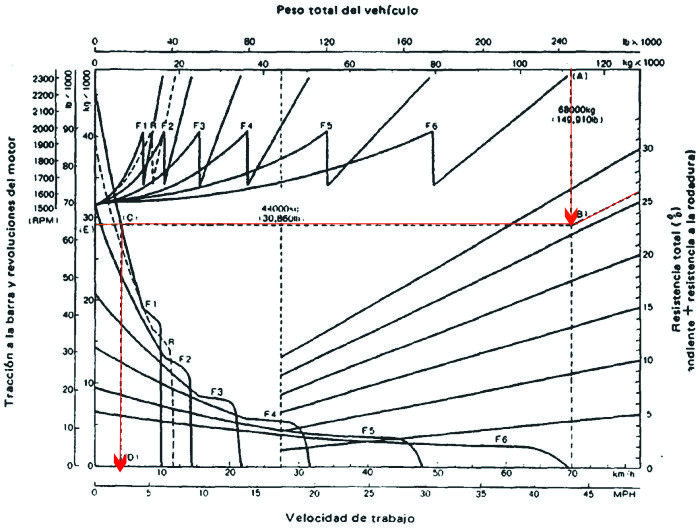
Para otro volquete del Gráfico No 2.3.4, también se puede calcular mediante un procedimiento análogo,la velocidad máxima y la tracción.
Con línea de trazos se indican los tres valores sobre dicha gr;afico, para un caso distinto con una pendiente compensada total del 26%, proporcionando los siguientes resultados : subirla en primera velocidad, a una velocidad máxima de 4.5 km/h y necesitaría una tracción mínima de 29200 kg.
Para los volquetes diesel eléctricos se dispone de curvas características algo distintas, pero cuyo empleo es análogo al descrito anteriormente, Gráfico No 2.3.5, aunque en este caso el gráfico está desdoblado en dos.
Gráfico No 2.3.5: Curva caracteristica de un volquete diesel eléctrico de 154 t (TEREX).
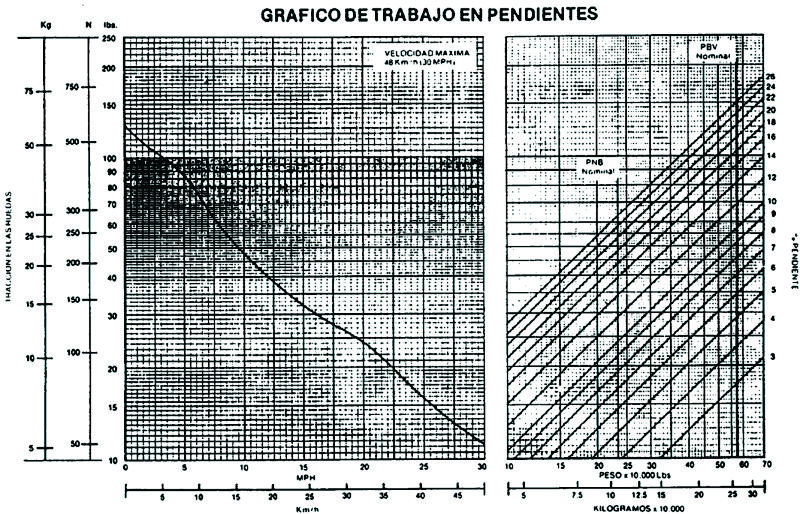
Para los volquetes diesel eléctricos se dispone curvas características algo distintas , pero cuyo empleo es análogo al descrito anteriormente , (Gráfico N° 2.3.5), aunque en este caso el gráfico está desdoblado en dos.
Con respecto a la tracción, conviene aclarar que el valor obtenido de las curvas características es un mínimo, y, por lo tanto, un factor limitador para los casos en los que el peso del volquete en las ruedas propulsoras multiplicado por el coeficiente del suelo no alcance este valor. Esta fuerza de tracción real no debe confundirse con la teórica de que dispone el volquete en función de su motor y sus rozamientos internos, que naturalmente será siempre mayor o igual que la real.
Cuando los vehículos descienden por rampas en lugar de remontarlas, el cálculo de las velocidades máximas no es tan sencillo, pues ya no es la máquina sólo la que responde a las condiciones de la pista, sino que el operador pasa a ser un factor fundamental.
Esto es así debido a que, cuando se remonta una pendiente, el operador sólo debe ocuparse de conectar la marcha adecuada y apretar el acelerador, e incluso con transmisión automática sólo acelerar, ya que la marcha adecuada se selecciona automáticamente. Pero para los descensos, el fabricante sólo recomienda una velocidad de descenso, en función de la capacidad de frenado y retardación del volquete. No obstante, el operador puede sentirse inseguro ante una velocidad excesiva y aminorar la marcha, modificando así los tiempos de viaje teóricos.
En los Gráficos No 2.3.6, 2.3.7 y 2.3.8 se representan tres gráficos de retardación de diferentes fabricantes en los que se ha señalado un ejemplo para mejor comprensión de su utilización.
Gráfico No 2.3.6: Curva característica de retardación de un volquete de 77 t de capacidad (CATERPILLAR).
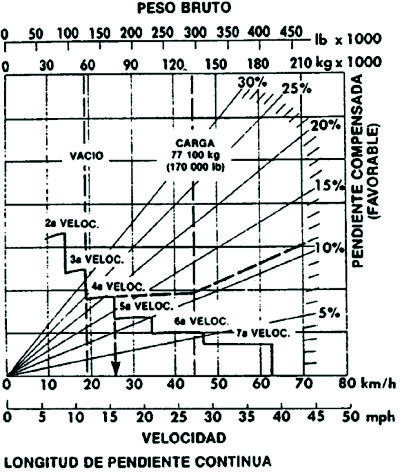
Gráfico No 2.3.7: Curva característica de retardación de un volquete de 68 t de capacidad (KOMATSU).

Gráfico No 2.3.8: Curva característica de retardación de un volquete diesel eléctrico de 154 t de capacidad (TEREX).
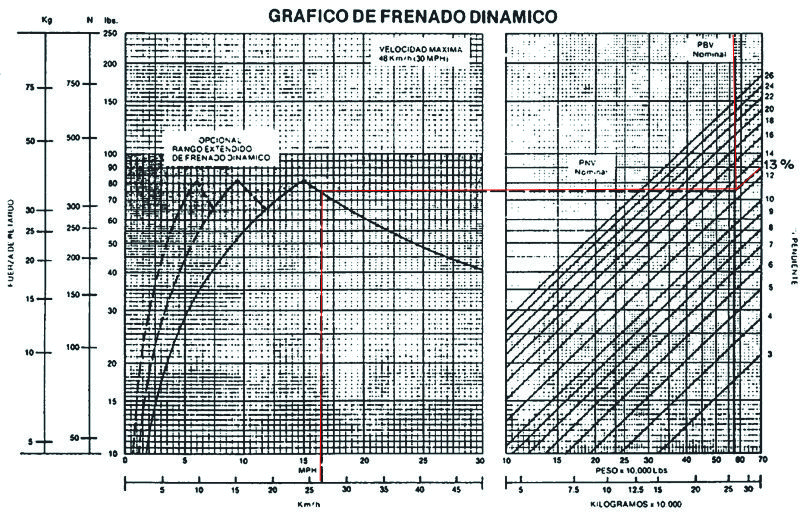
En los Gráficos No 2.3.6, 2.3.7 y 2.3.8 de retardación de diferentes fabricantes en los que se ha señalado un ejemplo para mejor comprensión de su utilización.
En todos los casos, el volquete baja una determinada pendiente llevando su carga nominal. En el caso del Gráfico No 2.3.6, para una pendiente compensada total del 10%, la velocidad máxima recomendada es de unos 26 km/h. En el caso del Gráfico No 2.3.7, la pendientecompensada total es algo mayor del 10% y la velocidad máxima recomendada es de 26 km/h aproximadamente, y por último en el Gráfico No 2.3.8, para una pendiente total del 13% se recomienda una velocidad de 27 km/h.
En algunos casos, si aparecen diferencias notables entre las velocidades recomendadas para distintos volquetes no debe extrañar, ya que puede tratarse de vehículos de carga muy distintos en cuanto a transmisión y retardador.
Igualmente, en el cálculo del tiempo de viaje habrán de introducirse correcciones por curvas muy pronunciadas, estrechamientos, lugares de escasa visibilidad, etc., aunque no se puede dar ninguna regla de valoración, ya que en cada caso concreto será diferente la repercusión sobre el tiempo total.
Algunos fabricantes proporcionan un método más simple de cálculo de los tiempos de recorrido, tanto con el volquete con su carga nominal, como vacío. Son sencillamente gráficos de espacio-tiempo de lectura directa, en los que se incluye una curva para cada pendiente total. Tienen el inconveniente de que sólo permiten calcular los tiempos de viaje para el equipo con su carga nominal o en vacío, pero no con una carga distinta.
En el Gráfico No 2.3.9 se representan dos de estas curvas para un volquete de 77 t de capacidad. En ambas se ha marcado un caso particular para un recorrido de 1500 m con pendiente adversa del 8%. Obsérvese que la diferencia de tiempo es de 2,6 minutos , lo que equivale a un 123% de aumento del tiempo de desplazamiento, al circular con carga en vez de en vacío, con esa misma pendiente adversa total.
Gráfico No 2.3.9: Tiempos de acarreo y retorno de un volquete de 77 t para diferentes distancias de transporte.

5.3.2.- Factores de velocidad.
Como ya se ha indicado, la velocidad obtenida mediante las curvas características es la máxima a la que se desplaza el equipo en cuestión en las condiciones indicadas. Para alcanzarla necesita una cierta longitud de pista, pudiendo luego mantenerla indefinidamente. Si la pista es suficientemente larga, se puede admitir esa velocidad como media para determinar el tiempo de trayecto, pero en tramos muy cortos la influencia del periodo de aceleración y deceleración es muy importante y habría que introducir las correcciones oportunas. Esto se lleva a cabo mediante los denominados "Factores de Velocidad".
Tabla No 2.3.5: Factores de Velocidad.
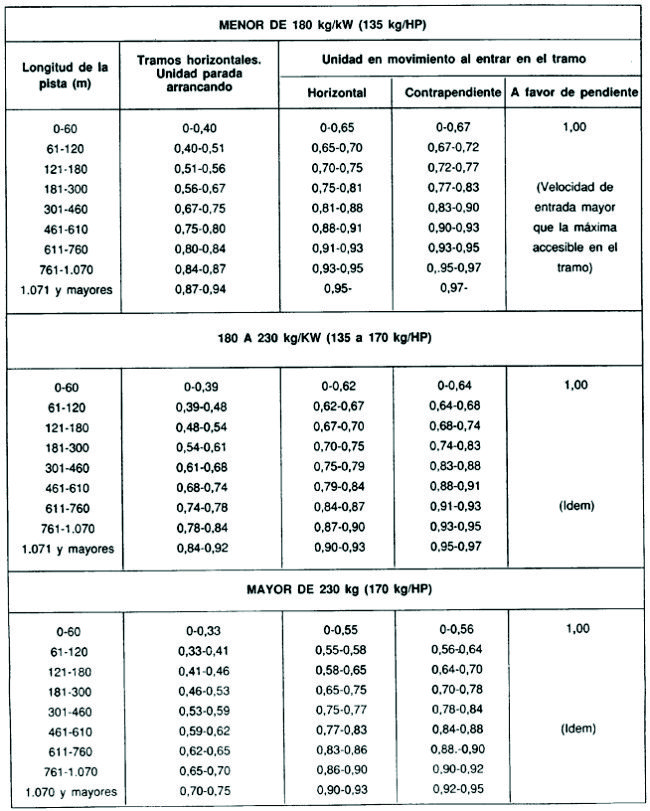
Para obtener los Factores de Velocidad, a partir de la Tabla 2.3.5, los pasos que es preciso dar son los siguientes:
Determinar la relación Peso/Potencia del equipo, expresada en kg/kW o kg/HP.
Elegir la columna apropiada según las condiciones de las que parte el vehículo.
Leer los Factores de Velocidad para la longitud del tramo de transporte considerado.
Usar un Factor de Velocidad de 1 para los volquetes que entren en un tramo con una velocidad próxima a la máxima y no sea el último tramo del perfil del recorrido.
Los Factores de Velocidad de los tramos finales del trayecto de ida, cuando el vehículo va cargado, serán tomados como equivalentes a los de la "Unidad parada arrancando".
La velocidad máxima alcanzable por un equipo en una pista se determinará a partir de la curva característica, y la velocidad media se obtendrá con la expresión:
Velocidad Media = Veloc. Máxima Alcanzable x Factor de Velocidad.
Para calcular el tiempo de transporte a lo largo de la pista se aplicará la ecuación:
Tiempo de transporte (min) = (Longitud de la pista (m) x 0,06)/(Velocidad media (km/h))
5.3.3.- Ejemplos.
Ejemplo de la aplicación de la resistencia total y tracción utilizable:
Problema: Se tiene un tractor de orugas (de 11 500 kg) que debe remolcar un tanque para agua, cuyo peso en vació es de 10 t y la carga permitida es de 30 t, deben desplazarse por un terreno con gravilla suelta; averiguar en qué cambios y velocidades debe desplazarse el tractor en un camino plano y si sería capaz de desplazarse con la carga por una pendiente de 60.
Solución
1).- Para el desplazamiento plano, sólo se averigua el valor de la resistencia al rodamiento del equipo que está remolcando, puesto que se esta haciendo con un tractor de orugas (despreciable la RR), ya que no hay resistencia a la pendiente.
Peso del tanque vacío = 10000 kg
Peso de la carga = 30000 kg
Peso total = 40000 kg
De la tabla de factores de resistencia a la rodadura:
Coeficiente de resistencia al rodamiento = 10/100 = 0.1
Resistencia al rodamiento = 40000*0.1 = 4000 kg
En la gráfica de las curvas de rendimiento de acarreo del tractor correspondiente se determinan las velocidades de desplazamiento para una fuerza de tracción en la barra de tiro de 4000 kg. La siguiente es una gráfica simulada, similar a las que dan los fabricantes
Gráfico No 2.3.4: Velocidades Vs Fuerza de tracciones a la barra de tiro
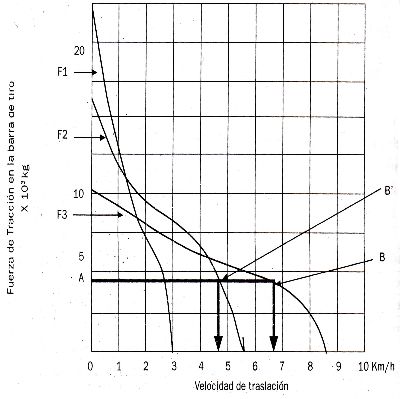
De acuerdo a la gráfica, se ubica el punto A en el eje Y, para una fuerza de tracción en la barra de tiro de 4000 kg, de este punto se traslada horizontalmente hasta encontrar la curva de engranajes correspondiente, el resultado es que el tractor puede desplazarse a 4.7 km/h en segunda (F2) punto B', o a 6.7 km/h en tercera (F3), punto B.
2).- Para averiguar si el equipo puede superar la pendiente se procede de la siguiente manera:
Primero se averigua la fuerza crítica de tracción en la barra de tiro.
El peso de operación del tractor es de 11500 kg, y en la tabla de coeficientes de tracción vemos que el coeficiente es de 0.50, por lo tanto:
Fuerza crítica de tracción en la barra de tiro = 11500*0.50 = 5750 kg
Luego se averigua la resistencia a la pendiente retardadora por cada ángulo de pendiente, para esto se suma todas las cargas, así:
Peso del tractor + peso del tanque + peso de la carga (agua) = 11500 + 10000 + 30000 = 51500 kg
por lo tanto la resistencia a la pendiente por ángulo de pendiente es 51500*0.018 = 927 kg (0.018 es el valor correspondiente a una pendiente de 10)
Capacidad para superar pendientes = (Fuerza crítica de tracción en la barra - RR)/(Resistencia a la pendiente por ángulo de pendiente) = (5750-4000)/(927) = 1.9 (grados)
Esta respuesta indica que el tractor con la carga que tiene que remolcar tan sólo puede superar una pendiente de 1.90, por lo tanto, la máquina no es apta para la pendiente de 60.